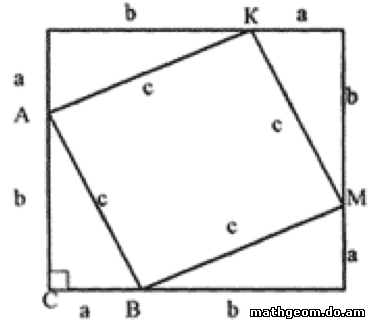
Теперь докажем теорему.Дано: АВС - треугольник, угол С=90°. АС, СВ - катеты, АВ - гипотенуза.
АС=b; СВ=а; АВ=с.
Доказать: а2 +b2 =с2
Доказательство:
Достроим треугольник АВС до квадрата.
Получим четыре равных прямоугольных треугольника (по 2-м катетам), отсюда следует, что гипотенузы равны. Четырехугольник АВМК - ромб.
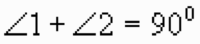т.к. треугольник АВС - прямоугольный., следовательно,
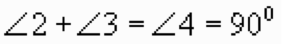
Если у ромба есть угол 90°, то такой ромб является квадратом: АВМК -квадрат.
Sб.кв.= (a+b)2 = a2 + 2ab + b2
Sб.кв.= 4S +SABKM = 4·1/2·(ab) +c2 = 2ab+c2.
Имеем: a2+2ab+b2=2ab+c2, т.е. a2+b2=c2
Теорема доказана.
| Страница 3 | Страница 4 | Страница 5 |