ЗАДАНИЕ 1: Сформулируйте основную идею предыдущего доказательства, затем запишите её в тетрадь.
Следствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.
Следствие 2. Если высоты двух треугольников равны, то и площади относятся как основания.
Запомни эти следствия, т.к. они в скором времени нам понадобятся.
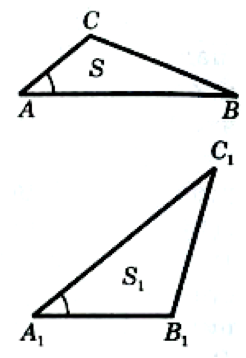Теорема. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.Доказательство:
Пусть S и S1 - площади треугольников ABC и A1B1C1, у которых
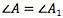(см. рис.). Докажем, что 
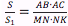.Наложим треугольник A1B1C1 на треугольник ABC так, чтобы вершина A1 совместилась с вершиной A, а стороны A1B1 и A1C1 наложились соответственно на лучи AB и
AC.
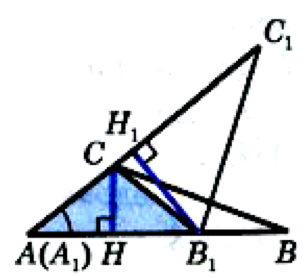
Треугольники АВС и AB1C имеют общую высоту – CH, поэтому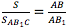 
по ______________ (какое следствие использовалось?).
Треугольники АВ1C и AB1C1 также имеют общую высоту – B1H1, поэтому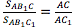
.
Перемножая полученные равенства, находим: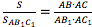
, или 
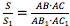.Теорема доказана!
ЗАДАНИЕ 2: Сформулируйте основную идею доказательства, затем запишите её в тетрадь.
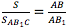по ______________ (какое следствие использовалось?).Треугольники АВ1C и AB1C1 также имеют общую высоту – B1H1, поэтому
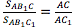.Перемножая полученные равенства, находим:
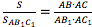, или 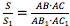.Теорема доказана!
ЗАДАНИЕ 2: Сформулируйте основную идею доказательства, затем запишите её в тетрадь.
| Страница 3 | Страница 4 |