Площадь параллелограмма
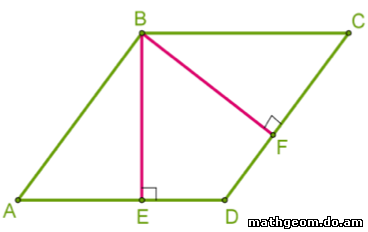
Можно ли построить параллелограмм с равными высотами? Какой вид такого параллелограмма? Так как стороны ромба одинаковы, то высоты ромба также одинаковы BE=BF.
Площадь произвольного параллелограмма
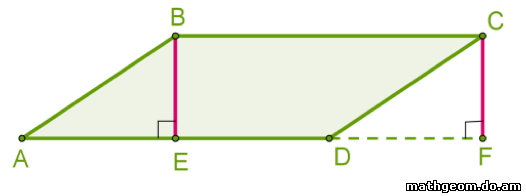Проведём высоты из двух вершин B и C к стороне AD.Прямоугольные треугольники ABE и DCF равны (равные гипотенузы как противоположные стороны параллелограмма и равные катеты как расстояние между параллельными прямыми).
Параллелограмм ABCD и прямоугольник EBCF — равновеликие, так как состоят из равных фигур:
SABCD = SABE + SEBCD
SEBCF = SEBCD + SDCF
Значит, площадь параллелограмма определяется так же, как площадь прямоугольника:
SEBCF = BE⋅BC
SABCD = BE⋅BC = BC⋅AD
Если обозначить сторону через a, высоту через h, то:
Sп−гр = a⋅h
Для определения площади параллелограмма можно использовать короткую сторону и высоту, проведённую к короткой стороне.
Найти стороны прямоугольника, если его площадь равна 48 см2, а одна сторона в 3 раза больше другой.
Сторона параллелограмма равна 12 см. Высота, опущенная на эту сторону равна 2 дм. Найдите площадь параллелограмма.
| Страница 2 | Страница 3 | Страница 4 |